音響設計学概説
3.振動と音
3.1 振動の基礎理論
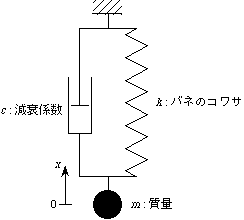
3.1.1 1自由度系の振動
自由振動
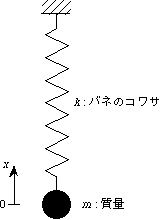
-
m = 1 [kg], c = 0.5 [N s/m], k = 40 [N/m], x0 = 0.1 [m] (減衰が弱い状態)
-
m = 0.2 [kg], c = 0.5 [N s/m], k = 40 [N/m], x0 = 0.1 [m] (減衰が弱い状態)
-
m = 1 [kg], c = 12 [N s/m], k = 40 [N/m], x0 = 0.1 [m] (臨界制動の状態)
-
m = 1 [kg], c = 20 [N s/m], k = 40 [N/m], x0 = 0.1 [m] (減衰が強い状態)
質点に交番振動(f Hz)をする外力が加わった場合
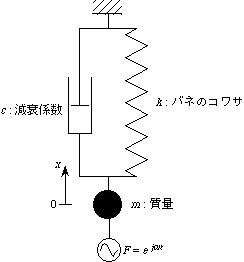
3.1.2 多自由度系の振動
自由振動
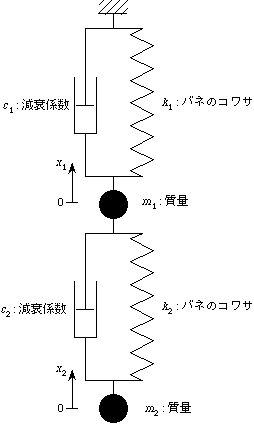
-
m1 = 1 [kg], k1 = 40 [N/m]
m2 = 1 [kg], k2 = 40 [N/m], x20 = 0.1 [m]
-
m1 = 1 [kg], k1 = 40 [N/m]
m2 = 0.2 [kg], k2 = 40 [N/m], x20 = 0.1 [m]
-
m1 = 1 [kg], c1 = 0.5 [N s/m], k1 = 40 [N/m]
m2 = 1 [kg], c2 = 0.5 [N s/m], k2 = 40 [N/m], x20 = 0.1 [m]
-
m1 = 1 [kg], c1 = 0.5 [N s/m], k1 = 40 [N/m]
m2 = 0.2 [kg], c2 = 0.5 [N s/m], k2 = 40 [N/m], x20 = 0.1 [m]
-
m1 = 1 [kg], k1 = 40 [N/m]
m2 = 1 [kg], k2 = 40 [N/m]
m3 = 1 [kg], k3 = 40 [N/m]
m4 = 1 [kg], k4 = 40 [N/m]
m5 = 1 [kg], k5 = 40 [N/m], x50 = 0.1 [m]
-
m1 = 1 [kg], c1 = 0.5 [N s/m], k1 = 40 [N/m]
m2 = 1 [kg], c2 = 0.5 [N s/m], k2 = 40 [N/m]
m3 = 1 [kg], c3 = 0.5 [N s/m], k3 = 40 [N/m]
m4 = 1 [kg], c4 = 0.5 [N s/m], k4 = 40 [N/m]
m5 = 1 [kg], c5 = 0.5 [N s/m], k5 = 40 [N/m], x50 = 0.1 [m]
3.2 発音体の振動
3.2.1 弦の振動

弦上の一点を引っぱって放す場合

-
r = 0.001 [kg/m], c = 200 [1/s], P = 100 [N], L = 1 [m], a = 0.5 [m], y0 = 0.1 [m]
-
r = 0.001 [kg/m], c = 200 [1/s], P = 100 [N], L = 1 [m], a = 0.25 [m], y0 = 0.1 [m]
-
r = 0.001 [kg/m], c = 500 [1/s], P = 100 [N], L = 1 [m], a = 0.25 [m], y0 = 0.1 [m]
-
r = 0.001 [kg/m], c = 200 [1/s], P = 100 [N], L = 1 [m], a = 0.143 [m], y0 = 0.1 [m]
弦上の一点に交番振動(f Hz)をする外力が加わった場合
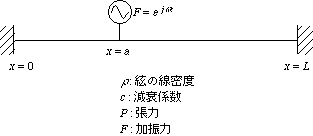
-
r = 0.001 [kg/m], c = 1500 [1/s], P = 100 [N], f = 250 [Hz], L = 1 [m], a = 0.25 [m]
-
r = 0.001 [kg/m], c = 1500 [1/s], P = 100 [N], f = 500 [Hz], L = 1 [m], a = 0.25 [m]
-
r = 0.001 [kg/m], c = 1500 [1/s], P = 100 [N], f = 1000 [Hz], L = 1 [m], a = 0.25 [m]
-
r = 0.001 [kg/m], c = 1500 [1/s], P = 100 [N], f = 158 [Hz], L = 1 [m], a = 0.25 [m]
弦を槌で打った場合

3.2.2 膜の振動
膜を槌で打った場合
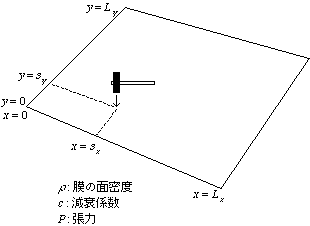
3.3 音から音場へ
3.3.1 固体の振動によって生ずる音場の解析法
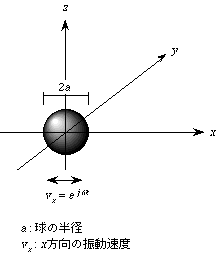
球の振動によって生ずる音場
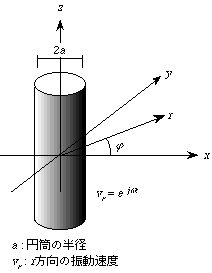
円筒形音源から放射される音場
3.3.2 障害物による散乱音場の解析法
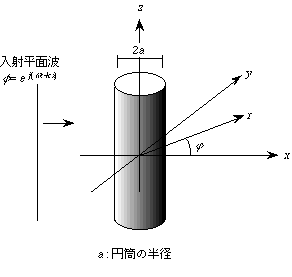
円筒による散乱音場
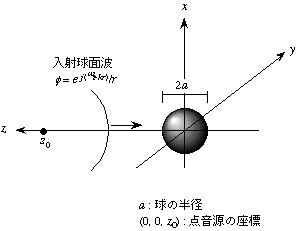
球による散乱音場
3.3.3 音場の数値解析
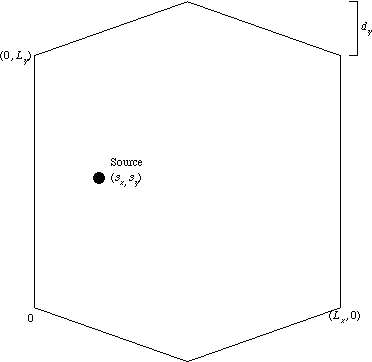
差分法による室内音圧分布変動の可視化
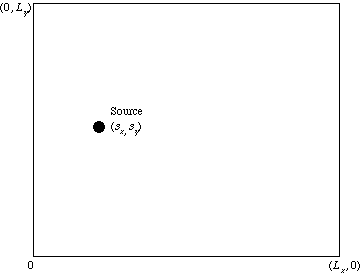
- Lx = 1.439 [m], Ly = 1.186 [m], dy = 0.25[m], sx = 0.3 [m], sy = 0.593 [m]
2 [fps]
6 [fps]
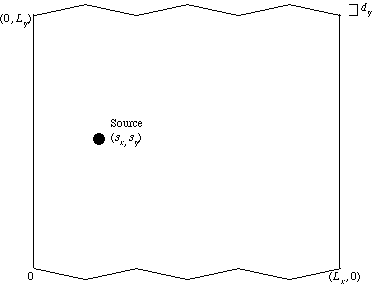
- Lx = 1.439 [m], Ly = 1.186 [m], dy = 0.08[m], sx = 0.3 [m], sy = 0.593 [m]
2 [fps]
6 [fps]
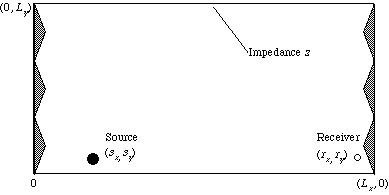
差分法による過渡応答の可聴化
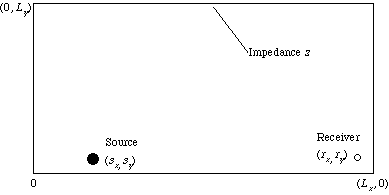
-
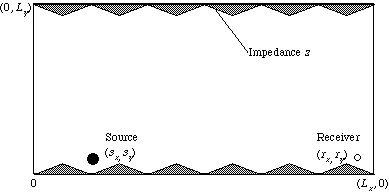
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m]
rx = 5.7 [m], ry = 0.3 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m]
rx = 5.7 [m], ry = 1.5 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m]
rx = 3 [m], ry = 2.7 [m]
-
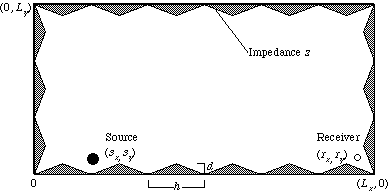
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], h = 1 [m], d = 0.2 [m]
rx = 5.7 [m], ry = 0.3 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], h = 1 [m], d = 0.2 [m]
rx = 5.7 [m], ry = 1.5 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], h = 1 [m], d = 0.2 [m]
rx = 3 [m], ry = 2.7 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], h = 1 [m], d = 0.2 [m]
rx = 5.7 [m], ry = 0.3 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], h = 1 [m], d = 0.2 [m]
rx = 5.7 [m], ry = 1.5 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], h = 1 [m], d = 0.2 [m]
rx = 3 [m], ry = 2.7 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], h = 1 [m], d = 0.2 [m]
rx = 5.7 [m], ry = 0.3 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], h = 1 [m], d = 0.2 [m]
rx = 5.7 [m], ry = 1.5 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], h = 1 [m], d = 0.2 [m]
rx = 3 [m], ry = 2.7 [m]
-
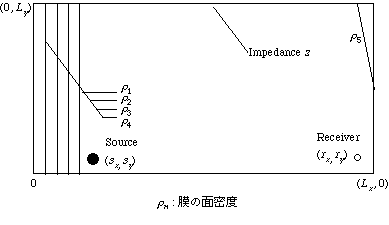
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], r1,2,3,4 = 0.3549 [kg/m2], r5 = 0.073 [kg/m2]
rx = 5.7 [m], ry = 0.3 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], r1,2,3,4 = 0.3549 [kg/m2], r5 = 0.073 [kg/m2]
rx = 5.7 [m], ry = 1.5 [m]
-
Lx = 6 [m], Ly = 3 [m], sx = 1 [m], sy = 0.3 [m], r1,2,3,4 = 0.3549 [kg/m2], r5 = 0.073 [kg/m2]
rx = 3 [m], ry = 2.7 [m]
Back to Toshiya SAMEJIMA's Lectures